8.7.-TRABALHO DE TRANSFORMAÇÃO

 Continuación =>
Até agora temos considerado que o trabalho e o esforço que uma unidade "i" precisa para tomar uma decisão é zero.
Isso na realidade não pode ser certo num Universo real.
Para aproximarmos um Universo das Decisões Ideal a um Universo Real, deveremos estudar os trabalhos de transformação.
Definimos Trabalho de Transformação como o esforço que uma unidade "i" tem que realizar para tomar uma decisão "s" .
 O trabalho de transformação 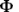vai depender do tipo de resposta da unidade "i".
Como temos visto em outros capítulos, uma decisão é tomada num intervalo de tempo,
T= @ + & + T'
Donde T´é o tempo que separa dois estímulos externos.
Vamos a considerar os caso nos quais esse tempo T' é igual a zero. Isso simplifica as expressões matemáticas e não implica nenhuma diferença com o caso no qual T' seja diferente de zero.
Por tanto.

T'= 0

E a expressão anterior fica como,

T= @ + &

Neste ponto teremos duas alternativas cuja diferença é apenas conceitual. Uma unidade "i" toma uma decisão num tempo mínimo @ e a executa num tempo &.
Como regra básica de nosso UD temos adotado que @ é um tempo mínimo constante e que & depende das características de cada unidade "i".
Poderíamos ter escolhido o contrario, quer dizer, que & fosse constante e o que variasse fosse @.. Eu não encontro diferenças, e salvo demonstrações em contrario, seguiremos com esse critério.
Porém uma vez adotado o critério, aparecem as conseqüências para cada um desses tempos.
Se @ é uma quantidade mínima e constante para o UD, ¿De que depende que varie &? Obviamente deve ser uma característica de cada um dos tipos de Unidades "i" e deve depender da quantidade de Energia que cada Tipo de unidade "i" tem acumulada.


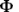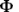Teremos então que, o Trabalho de Transformação pode ser decomposto em dois trabalhos. O Trabalho de Decisão (@) e o Trabalho de Execução (&).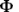
O Trabalho de Decisão 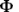(@) é o trabalho necessário para produzir uma decisão "s" num tempo constante @. Esse trabalho depende de que tipo de decisão se toma.
O Trabalho de Execução 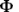(&) é o trabalho necessário para executar uma decisão "s" num tempo variável & que depende da quantidade de energia que cada Tipo de Unidade "i" tem.

F = (@) + (&)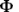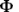

Esta distinção é fundamental. Por um lado, segundo o tipo de decisão que uma Unidade "i" pode tomar, se condiciona que quantidade de energia tem que ter como mínimo, para tomar ao menos uma decisão desse tipo. Essa quantidade de energia é determinada por (@).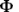
Dependendo de como seja 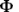(@), uma unidade "i" terá como mínimo uma quantidade de energia que determinará o tempo de execução & e por  tanto (&).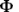
Uma vez determinada essa quantidade, teremos que ver que combinações de unidades "i" podem fazer que um tipo determinado de decisões se tomem de forma estável. Essa combinação de unidades "i" darão lugar ás partículas possíveis no Universo Real.

Nota do Autor:

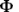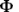Meu trabalho se encontra em este ponto ao final de ano 2002. Pretendo demonstrar que (&) produz os movimentos das unidades "i" equivalentes ao que conhecemos como atração gravitacional. Enquanto que (@) produz o resto dos fenômenos atribuídos ao que no Universo Real conhecemos como conseqüência dos campos elétricos, magnéticos e de interação forte dentro do núcleo.


Próxima Página