8.1.-MOVIMENTO UNIFORME: |
Continuação => |
| Imaginemos um
corpo composto por uma única unidade i(0) situada na origem de
coordenadas E1(0),E2(0),E3(0),....En(0), que toma decisões
iguais a respeito a um único estímulo proposto por uma unidade
i(1) com coordenadas Então, En(0)=En(1) para valores n=2 a n=n E alem disso, ao serem iguais todas as decisões que toma referidas à mesma proposta, se supomos que essa decisão sempre igual é "a" que representamos sua quantidade no eixo X de coordenadas. E1,e(0)=E1,z(0)=0 Então esta situação corresponderia ao modelo mais básico que podemos imaginar e podemos representa-lo dentro do mesmo eixo de coordenadas. 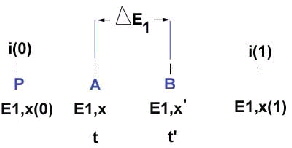 Supondo que no tempo t a unidade i(0) tem tido uma quantidade de decisões E1, x a respeito a i(1) Ponto A do eixo E1,x Mais tarde no tempo t', tem tido x' decisões. Ponto B do eixo E1,x Então. PA= E1,x PB= E1,x' Aonde, é o incremento das decisões que teve a unidade i(0) no incremento de tempo, A velocidade média da unidade i(0) a respeito à unidade i(1) vem definido por: 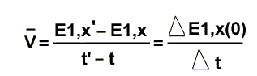 Conseqüentemente a velocidade média durante um certo intervalo de tempo é igual às decisões médias tomadas por unidade de tempo. Para determinar a velocidade instantânea em um ponto, tal como A, devemos fazer o intervalo de tempo Dt tão pequeno como seja possível, de modo que essencialmente não ocorram mudanças no estado das decisões durante esse pequeno intervalo. Na linguagem matemática este é equivalente a calcular o valor do limite da fração anterior quando o denominador Dt tende a zero. 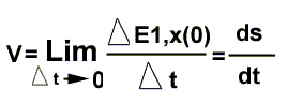 Esta é a definição de derivada de s com respeito ao tempo t. Próxima Página |
|